Finite Difference Approximation

Next: Dynamics Restarts Up: Cartesian Coordinate Space Previous: Temperature Coupling

Finite Difference Approximation

X-PLOR makes use of a third-order finite difference approximation in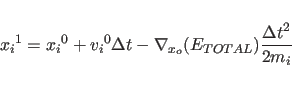

(Brünger, Brooks, and Karplus, 1984). First, the initial coordinates ${x_i}^0$ are subjected to the SHAKE method. Then the system gets the initial velocities ${v_i}^0$ . Next, the program prints the energy of the initial coordinates. A two-step method is used to obtain the coordinates ${x_i}^1$ :

$\begin{displaymath} {x_i}^1 = {x_i}^0 + {v_i}^0 \Delta t - {\nabla}_{x_o}(E_{TOTAL}) {{\Delta t}^2 \over 2 m_i} \end{displaymath}$

(11.8)

IF SHAKE constraints are present, the SHAKE method is applied to ${x_i}^1$ with respect to ${x_i}^0$ .

Iteration from step to step causes $(x_i^{n-1} , x_i^n) \longrightarrow (x_i^{n+1} , v_i^n)$ . The algorithm computes the forces $F_i^n=-{\nabla}_{x_i^n}E + f_i(t)$ . The algorithm then computes

$\begin{displaymath} x_i^{n+1} = [1 + {b_i \Delta t \over 2}] ^{-1} [ 2 x_i^n - x... ...Delta t}^2 \over m_i} + x_i^{n-1} ({b_i {\Delta t} \over 2}) ] \end{displaymath}$

(11.9)

If required, the SHAKE method is applied to $x_i^{n+1}$ with

as the reference set. Finally, the velocities at this step are computed:

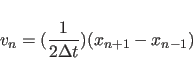$\begin{displaymath} v_n = ( {1 \over 2 \Delta t} ) ( x_{n+1} - x_{n-1} ) \end{displaymath}$

(11.10)

(The velocities do not enter the equations to compute the trajectory

.) In case of zero friction coefficients

, this algorithm reduces to the three-step Verlet method (Verlet, 1967).

Xplor-NIH 2025-03-21