| bit | Xplor-NIH | VMD-XPLOR |
|---|
|
| Xplor-NIH home Documentation |
Next: Syntax Up: Restraints Associated with Paramagnetic Previous: Restraints Associated with Paramagnetic
Paramagnetic Relaxation Enhancement Restraints
Paramagnetic relaxation enhancement can be used to derive a distance
estimate. The transverse relaxation rate is given by the
Solomon-Bloembergen equation:
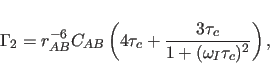 |
(34.1) |
The energy term takes the form
![\begin{displaymath}
E_{PMAG}=K_{PMAG} (\Gamma_2^{calc}-\Gamma_2^{obs})^2
\left[...
...amma_2^{obs}}{\sqrt{2}\sigma_\Gamma}\right)^2\right]
\right],
\end{displaymath}](img774.png) |
(34.2) |
See Donaldson et al. (2001) for more information.
Subsections
Xplor-NIH 2025-11-07
