U.S. flag

An official website of the United States government
  next up previous contents index  Xplor-NIH home Documentation

Next: Velocity Assignment Up: Cartesian Coordinate Space Previous: Cartesian Coordinate Space


Simple Langevin Dynamics

X-PLOR provides the possibility of carrying out Langevin dynamics. The simple Langevin equation has the form
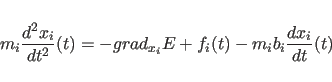\begin{displaymath} m_i{d^2x_i \over dt^2}(t) = -grad_{x_i}E + f_i(t) - m_i b_i{dx_i \over dt}(t) \end{displaymath} (11.2)

where the random force $f_i(t)$ is derived from a Gaussian distribution with the properties
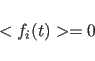\begin{displaymath} <f_i(t)>=0 \end{displaymath} (11.3)


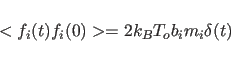\begin{displaymath} <f_i(t)f_i(0)> = 2 k_B T_o b_i m_i \delta(t) \end{displaymath} (11.4)

where $k_B$ is Boltzmann's constant and $T_o$ is the temperature specified by TBATh. For Langevin heatbath applications, the total energy $E_{TOTAL}$ can be augmented by a harmonic energy term for all atoms with a nonzero friction coefficient $b_i$. The setup of the harmonic energy is described in Section 7.1. The friction coefficient $b_i$ is defined by assigning the FBETa atom property (see Section 2.16). Langevin dynamics is used for all atoms that have nonzero friction coefficients $b_i$ and that are outside a sphere with radius RBUF (default 0) around the origin ORIGIn. This check is carried out periodically (ILBFrq parameter). By default the atom property FBETa is zero; i.e., all atoms are treated as normal particles.

next up previous contents index
Next: Velocity Assignment Up: Cartesian Coordinate Space Previous: Cartesian Coordinate Space   Contents   Index
Xplor-NIH 2024-09-13