| bit | Xplor-NIH | VMD-XPLOR |
|---|
|
| Xplor-NIH home Documentation |
Next: Dynamics Restarts Up: Cartesian Coordinate Space Previous: Temperature Coupling
Finite Difference Approximation
X-PLOR makes use of a third-order
finite difference approximation in 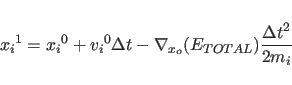 |
(11.8) |
Iteration from step ![]() to step
to step ![]() causes
causes
![]() .
The algorithm computes the forces
.
The algorithm computes the forces
![]() .
The algorithm then computes
.
The algorithm then computes
![\begin{displaymath}
x_i^{n+1} = [1 + {b_i \Delta t \over 2}] ^{-1} [ 2 x_i^n - x...
...Delta t}^2 \over m_i} + x_i^{n-1} ({b_i {\Delta t} \over 2}) ]
\end{displaymath}](img302.png) |
(11.9) |
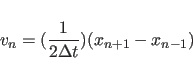 |
(11.10) |
Xplor-NIH 2025-11-07
