Next: Syntax Up: Crystallographic Refinement Previous: Rigid-Body Refinement

Overall B-Factor Refinement

The xrefin optimize overall statement optimizes overall isotropic or anisotropic B-factors by employing a conjugate gradient minimization using $E_{XREF}$ (Eq. 13.1) as the target. For the isotropic case, the variable is simply the overall B-factor

, and $F_{calc}(\vec{h})$ in Eq. 13.1 is replaced by

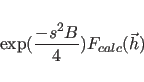$\begin{displaymath} \exp({\frac{-s^2B}{4}}) F_{calc}({\vec h}) \end{displaymath}$

(14.1)

For the anisotropic case, the variables are the six parameters of the anisotropic B-factor tensor $B_{ij}$ , and $F_{calc}(\vec{h})$ in Eq. 13.1 is replaced by

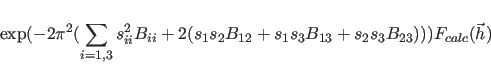$\begin{displaymath} \exp(-2 {\pi}^2 ( \sum_{i=1,3} s_{ii}^2 B_{ii} + 2( s_1 s_... ...2} + s_1 s_3 B_{13} + s_2 s_3 B_{23} ) )) F_{calc}({\vec h}) \end{displaymath}$

(14.2)

Note that $F_{part}$ is not touched during this procedure, but it is still added to the modified $F_{calc}$ terms to yield

After termination, the procedure multiplies the $F_{calc}$ structure factors with the overall B-factor shift. In the isotropic case, it also adds the refined B-factor shift to the coordinate array Bs. The $F_{calc}$ structure factors must be computed prior to invoking this routine, e.g., through the UPDAte xrefin statement.

Subsections

Xplor-NIH 2025-03-21