Computation of Electron Density Maps of a helical structure

Next: Syntax Up: Fiber Structure Refinement Previous: Requirements

Computation of Electron Density Maps of a helical structure

The fiber_refin-map-statement can be used to calculate electron density maps, which can be calculated by a Bessel-Fourier transform of $_{nl}(R)$ :

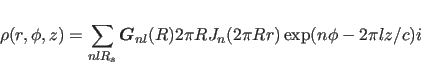$\begin{displaymath} \rho (r, \phi, z) = \sum_{nlR_s} \mbox{\boldmath$G$}_{nl}(R) 2\pi R J_{n}(2\pi R r) \exp(n\phi-2\pi lz/c)i \end{displaymath}$

(15.10)

To reduce the computational time, a factorization method which is similar to the Beevers-Lipson factorization method is applied to the Bessel-Fourier transform. The first step is an one-dimensional Bessel transform:

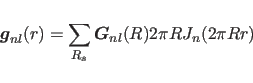$\begin{displaymath} \mbox{\boldmath$g$}_{nl} (r) = \sum_{R_s} \mbox{\boldmath $G$}_{nl} (R) 2\pi R J_{n}(2\pi R r) \end{displaymath}$

(15.11)

Because the electron density map is usually rendered in the orthogonal space, coefficient

$_{nl} (r)$ is converted from the cylindrical space into the orthogonal space in the Fourier transform:

$\displaystyle \mbox{\boldmath$S$}_l (xy)$	$\textstyle =$	$\displaystyle \sum_{n} \mbox{\boldmath$g$}_{nl}(r) \exp (n\phi)i$
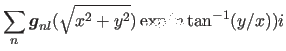	$\textstyle =$	$\displaystyle \sum_{n} \mbox{\boldmath$g$}_{nl} (\sqrt{x^2+y^2}) \exp (n \tan^{-1} (y/x))i$	(15.12)

The Fourier transform of

in the final step yields the electron density map:

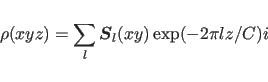$\begin{displaymath} \rho (xyz) = \sum_l \mbox{\boldmath$S$}_l (xy) \exp (-2\pi lz/C)i \end{displaymath}$

(15.13)

Subsections

Xplor-NIH 2025-03-21