Symmetry Function

Next: 3D NOE-NOE Function Up: Choice of Restraining Functions Previous: Soft-Square Function

Symmetry Function

For POTEntial=SYMMetry, a soft-square function (Eq. 20.12) is used to restrain signed distance differences to specified values. The two distances are specified by a pair of ASSIgn statements:

$\begin{eqnarray*} & & {\tt assign \quad <selection> \quad <selection> } \quad d ... ...n \quad <selection> \quad <selection> } \quad 0 \quad 0 \quad 0 \end{eqnarray*}$

The second distance of a given pair of distances is subtracted from the first; the distance difference can have negative values. The functional form is similar to the soft-square function (Section 20.3.4), except that the switching region is symmetrically arranged around the ideal distance difference (i.e., the program switches to the soft asymptote for $R > d+d_{plus}-d_{off} + r_{sw}$ as well as for $R < d-d_{minus} - r_{sw}$ ) and $\Delta$ is defined as

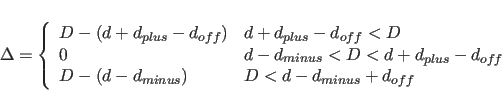
$\begin{displaymath} \Delta = \left\{ \begin{array}{ll} D-(d+d_{plus}-d_{off}) &... ...us}) & \mbox{$D < d-d_{minus}+d_{off}$} \end{array} \right. \end{displaymath}$

(20.13)

where

denotes the distance difference

between the two assigned distances. The distances

and

are obtained by various averaging methods as described in Section 20.2.

Xplor-NIH 2024-09-13