3D NOE-NOE Function

For POTEntial=3DPO, a restraining function for 3D NOE-NOE experiments is used. The intensity of a 3D NOE-NOE crosspeak, $I_{ijk}(\tau_{m1},\tau_{m2})$, between spins $i,j$, and $k$, is proportional to the product of the individual NOE transfer efficiencies of each mixing time:

$$I_{ijk}(\tau_{m1},\tau_{m2}) = c[exp(-{\bf R}\tau_{m2})]_{ij} [\exp(-{\bf R} \tau_{m1})]_{jk}A_{kk}(0),$$ (20.14)

where $\tau_{m1}$ is the first and $\tau_{m2}$ the second mixing time, R the cross-relaxation matrix, $A_{kk}(0)$ the equilibrium magnetization of spins $k$, and $c$ a constant.

The 3D NOE-NOE intensity can be approximated by

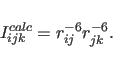$$I_{ijk}^{calc} = r_{ij}^{-6} r_{jk}^{-6}.$$ (20.15)

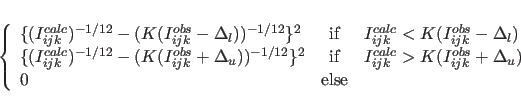
where $r_{ij}$ and $r_{jk}$ are the distances between spins $i,j$ and $j, k$, respectively, and the proportionality constant is set equal to one. The 3D NOE-NOE function is given by

$$E_{NOE}^{class} = S \times$$ (20.16)

$$\left\{ \begin{array}{lcl} \{(I_{ijk}^{calc})^{-1/12} - (K(... ...^{obs}+\Delta_{u}) \\ 0 & {\rm else} & \\ \end{array}\right.$$

where $S$ is the energy constant specified by the SCALe statement, $I_{ijk}^{obs}$ is the observed NOE-NOE intensities, $\Delta_{l}$ and $\Delta_{u}$ are error bounds, and $K$ is a scale factor specified by the RSWITch statement. The NOE-NOE connectivity $i \rightarrow j \rightarrow k$ and the intensity and error-bound information are provided by a pair of ASSIgn statements:

$$\begin{eqnarray*} & & {\tt assign } \quad ( {\rm spin}_i ) \quad ( {\rm spin}_j ... ...{\rm spin}_j ) \quad ( {\rm spin}_k ) \quad 0 \quad 0 \quad 0 \end{eqnarray*}$$

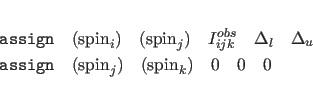
The first ASSIgn statement specifies spins $i$ and $j$, along with the observed intensity $I_{ijk}^{obs}$ and the error bounds $\Delta_{l}$ and $\Delta_{u}$. The second ASSIgn statement specifies spins $j$ and $k$; the three real numbers following the second selection are irrelevant and can be set to arbitrary values. Note: the 3D NOE-NOE function can be used in combination with R-6 or center averaging. For further details, the reader is referred to Habazettl et al. (1992b,a) and Bernstein et al. (1993).