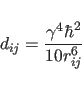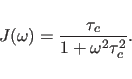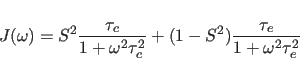Next: Analytical Expression for the Up: NMR Back-calculation Refinement Previous: Output

The Relaxation Matrix

The basis for the refinement is the calculation of the volume of a cross peak between spins

and

, $I_{ij}^{c}$ , from the atomic coordinates by means of the relaxation matrix R (Ernst, Bodenhausen, Wokaun, 1987; Macura and Ernst, 1980) (Keepers and James 1984):

$\begin{displaymath} I_{ij}^{c} \propto [\exp(-{\bf R} \tau_{m})]_{ij}, \end{displaymath}$

(39.1)

where $\tau_{m}$ is the mixing time. The relaxation matrix R is a function of the transition rates $\Omega^{ij}$

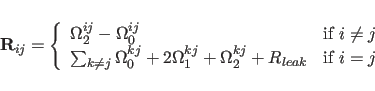$\begin{displaymath} {\bf R}_{ij} = \left\{ \begin{array}{ll} \Omega_{2}^{ij}... ...2}^{kj} + R_{leak} &\mbox{if $i = j$} \\ \end{array}\right. \end{displaymath}$

(39.2)

which are determined by spectral densities and dipolar coupling strengths (Solomon, 1955):

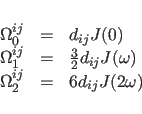$\begin{displaymath} \begin{array}{lcl} \Omega_{0}^{ij} &= &d_{ij} J(0) \\ \Omeg... ...a) \\ \Omega_{2}^{ij} &= &6 d_{ij} J(2 \omega) \\ \end{array}\end{displaymath}$

(39.3)

and

$\begin{displaymath} d_{ij} = \frac{\gamma^{4} \hbar^{2}}{10 r_{ij}^{6}} \end{displaymath}$

(39.4)

$\gamma$ is the gyromagnetic ratio of the proton and $r_{ij}$ the distance between spins

and

. At present, only protons can be used in the refinement. $R_{leak}$ describes the non-NOE magnetization losses from the lattice.

In the simplest model, it is assumed that a single isotropic correlation time $\tau_{c}$ is sufficient to describe the spectral densities $J(\omega)$ (Solomon, 1955):

$\begin{displaymath} J(\omega) = \frac{\tau_{c}}{1+\omega^{2}\tau_{c}^{2}}. \end{displaymath}$

(39.5)

A step beyond this simple model is the “model-free" approach of Lipari and Szabo (1982), where the internal motion is described by two parameters, an effective correlation time $\tau_{e}$ and an order parameter :

$\begin{displaymath} J(\omega) = S^2 \frac{\tau_{c}}{1+\omega^{2}\tau_{c}^{2}} + (1-S^2) \frac{\tau_{e}}{1+\omega^{2}\tau_{e}^{2}} \end{displaymath}$

(39.6)

X-PLOR uses an approximation of this equation that assumes that the internal motion is much faster than the overall rotation of the molecule (i.e., $\tau_{e} \ll \tau_{c}$ ), such that the second term in the equation becomes negligible. In order to take into account the different motional behavior of different parts of the molecule, different correlation time and order parameters can be entered for different proton-proton vectors.

Groups of protons whose resonances are degenerate due to motion (in general, mostly methyl groups) are treated roughly as in CORMA, version 1.5 (Keepers and James 1984). (Note that cross peaks which are ambiguous due to overlap should be dealt with in a different way; see the example input file in Section 39.7.) Each such group is represented by one spin, whose intensity is scaled by the number of protons in the group, and the distance to the group is calculated as the $<r^{-3}>^{-1/3}$ or $<r^{-6}>^{-1/6}$ average over the protons in the group (Eq. 39.4). In addition, a diagonal leakage rate is added for each group of protons.

Protons can be removed from the spin system (exchangeable protons in DO spectra, deuterium-labeled molecules), or their appropriate occupancy can be specified (exchangeable protons in HO spectra).

Xplor-NIH 2024-09-13