| bit | Xplor-NIH | VMD-XPLOR |
|---|
|
| Xplor-NIH home Documentation |
Next: The Energy Term Up: NMR Back-calculation Refinement Previous: The Relaxation Matrix
Analytical Expression for the Gradient
The derivative of where
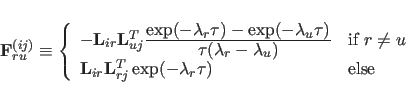 |
(39.8) |
Xplor-NIH 2025-11-07

![\begin{displaymath}
{\bf\nabla}_{\mu} I_{ij}^{c} =
{\bf\nabla}_{\mu}[\exp(- {\bf...
...({\bf\nabla}_{\mu}{\bf R}) {\bf L} {\bf F}^{(ij)} {\bf L}^{T}]
\end{displaymath}](img818.png)