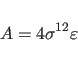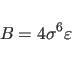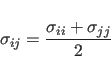| bit | Xplor-NIH | VMD-XPLOR |
|---|
|
| Xplor-NIH home Documentation |
Next: Electrostatic Function Up: Nonbonded Energy Terms Previous: Nonbonded Energy Terms
Van der Waals Function
The van der Waals function is given by
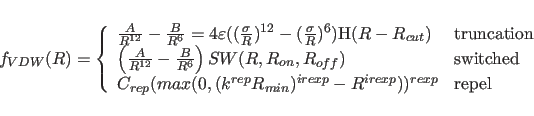
where
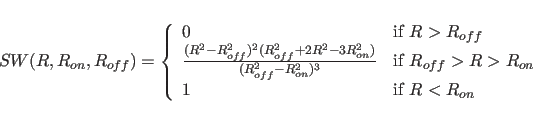
For both the truncated and the switched option, the van der Waals function is described by a Lennard-Jones potential. In this potential, the attractive force is proportional to
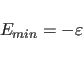 |
(4.11) |
The repel option uses a simple repulsive potential. It is used primarily for structure refinements with X-ray crystallographic and solution NMR spectroscopic data.
The NBON statement (Section 3.2.1) defines
![]() for the Lennard-Jones potential between identical atom
types. Between different atom types, the following combination rule is used
by default:
for the Lennard-Jones potential between identical atom
types. Between different atom types, the following combination rule is used
by default:
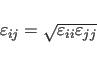 |
(4.15) |
The NBFix statement allows
one to deviate from this combination rule; i.e,
one can explicitly specify the ![]() coefficients for an atom type pair
(see Section 3.2.1).
coefficients for an atom type pair
(see Section 3.2.1).
Minimization of the empirical potential energy for initial coordinates with very close nonbonded contacts is often ill behaved because the Lennard-Jones potential produces a very large gradient reflecting the close contacts. To avoid this problem, the Lennard-Jones and electrostatic potential can be replaced with the repel potential, which is softer and purely repulsive.
Xplor-NIH 2025-11-07

![\begin{displaymath}
R_{min} = \sigma \sqrt[6]{2}
\end{displaymath}](img178.png)