| bit | Xplor-NIH | VMD-XPLOR |
|---|
|
| Xplor-NIH home Documentation |
Next: Iteration Up: Rigid-Body Coordinate Space Previous: Rigid-Body Coordinate Space
Initialization
Each inertia tensor is diagonalized by a rotational transformation to the body coordinate system: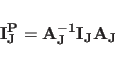 |
(11.14) |
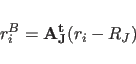 |
(11.15) |
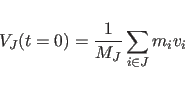 |
(11.16) |
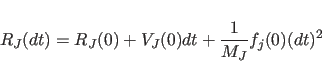 |
(11.17) |
The more stable Euler-Cayley
parameters (also referred to as quaternions)
are used as rotational variables instead of the Euler angles ![]() ,
,
![]() ,
, ![]() (cf. Goldstein (1980)).
They are defined in
Eq. 2.1.
The quaternions
are initialized using a first-order approximation to their equation of
motion:
(cf. Goldstein (1980)).
They are defined in
Eq. 2.1.
The quaternions
are initialized using a first-order approximation to their equation of
motion:
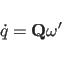 |
(11.18) |
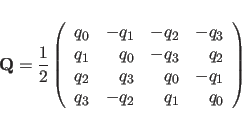 |
(11.19) |
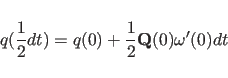 |
(11.20) |
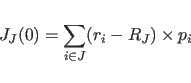 |
(11.21) |
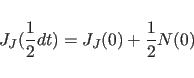 |
(11.22) |
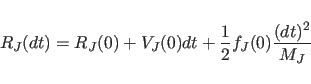 |
(11.23) |
Xplor-NIH 2025-11-07
