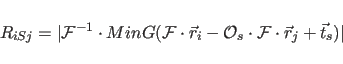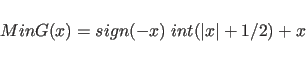Crystallographic Symmetry Interactions

Next: Non-crystallographic Symmetry Interactions Up: Nonbonded Energy Terms Previous: Intramolecular Interactions

Crystallographic Symmetry Interactions

Crystallographic symmetry interactions (e.g., packing interactions) between the molecule(s) located in the asymmetric unit and all symmetry-related molecules surrounding the asymmetric unit are computed by

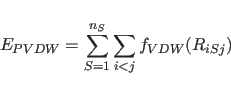$\begin{displaymath} E_{PVDW} = \sum^{n_{S}}_{S=1} \sum_{i<j} f_{VDW}(R_{iSj}) \end{displaymath}$

(4.19)

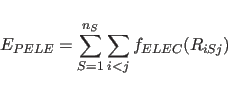$\begin{displaymath} E_{PELE} = \sum^{n_{S}}_{S=1} \sum_{i<j} f_{ELEC}(R_{iSj}) \end{displaymath}$

(4.20)

where the first sum extends over all cystallographic symmetry operators ( ${\cal O}_{s}, \vec{t}_{s}$ ) and $R_{iSj}$ is defined by

$\begin{displaymath} R_{iSj}= \vert {\cal F}^{-1} \cdot MinG( {\cal F} \cdot \v... ...l O}_s \cdot {\cal F} \cdot \vec{r}_{j} + \vec{t}_s ) \vert \end{displaymath}$

(4.21)

${\cal F}$ is the matrix that converts orthogonal coordinates into fractional coordinates, and the second sum extends over all pairs of atoms

for which $R_{i}s_{j}$ is less then a specified cutoff selected by the constraints interaction statement $r_{cut}$ and

and

are the coordinates. The function $MinG(\vec{r})$ defines the minimum image distance in fractional coordinate space. It operates separately on each component of the three-dimensional vector $\vec{r}$ , where the operation on each component

is given by

$\begin{displaymath} MinG(x)= sign(-x) \; int(\vert x\vert + 1/2) + x \end{displaymath}$

(4.22)

The function

is defined as the integer part of x, and

is defined as the sign of x. The nonbonding interaction energy between two atoms is independent of whether it is an intermolecular or an intramolecular interaction. The atom/group search and the update of the interaction list are carried out analogously to the intramolecular case. (Refer to Section 13.3 for the definition of symmetry operators and the unit-cell constants that define ${\cal F}$ .)

Xplor-NIH 2025-03-21