Initialization

Next: Iteration Up: Rigid-Body Coordinate Space Previous: Rigid-Body Coordinate Space

Initialization

Each inertia tensor is diagonalized by a rotational transformation to the body coordinate system: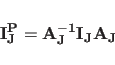

$\begin{displaymath} {\bf I^P_{J}=A^{-1}_{J}I_JA_J} \end{displaymath}$

(11.14)

The transformation matrix ${\bf A_J}$ is used to initialize rotational variables such that ${\bf A_J}$ = ${\bf (A^{-1}_{J})^t}$ . Values for the body-frame coordinates $r^B_{i}$ of group elements are obtained by

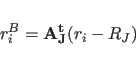$\begin{displaymath} r^B_{i}={\bf A^t_{J}}(r_i-R_J) \end{displaymath}$

(11.15)

The net force and torque acting on each body are determined by summing the force and torque acting on each of its constituent atoms. Center-of-mass variables are initialized with a two-step process. The initial center-of-mass velocities are determined from the atom properties VX,VY,VZ:

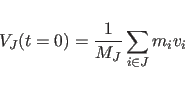$\begin{displaymath} V_J(t=0)={1\over M_J}\sum_{i\in J} m_iv_i \end{displaymath}$

(11.16)

These velocities are then used to advance the center-of-mass coordinates

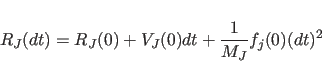$\begin{displaymath} R_J(dt)=R_J(0)+V_J(0)dt+{1\over M_J}f_j(0)(dt)^2 \end{displaymath}$

(11.17)

The more stable Euler-Cayley parameters (also referred to as quaternions) are used as rotational variables instead of the Euler angles $\theta_1$ , $\theta_2$ , $\theta_3$ (cf. Goldstein (1980)). They are defined in Eq. 2.1. The quaternions are initialized using a first-order approximation to their equation of motion:

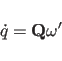$\begin{displaymath} \dot{q}={\bf Q}\omega' \end{displaymath}$

(11.18)

where $\dot{q}$ is the four-vector ( $\dot{q}_0$ , $\dot{q}_1$ , $\dot{q}_2$ , $\dot{q}_3$ ), $\omega'$ is the four-vector (0, $\omega_x$ , $\omega_y$ , $\omega_z$ ), and ${\bf Q}$ is the matrix that gives their time evolution:

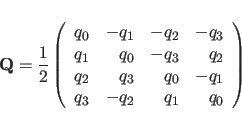$\begin{displaymath} {\bf Q}={1\over 2}\left(\begin{array}{rrrr} q_0 & -q_1 & -q... ...3 & q_0 & -q_1 \\ q_3 & -q_2 & q_1 & q_0 \end{array} \right) \end{displaymath}$

(11.19)

Thus one obtains

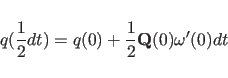$\begin{displaymath} q({1\over 2}dt)=q(0)+{1\over 2}{\bf Q}(0)\omega'(0)dt \end{displaymath}$

(11.20)

The initial angular velocity $\omega$ follows directly from the initial angular momentum, which is determined by

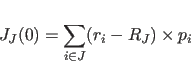$\begin{displaymath} J_J(0)=\sum_{i\in J} (r_i-R_J)\times p_i \end{displaymath}$

(11.21)

where

is the momentum of the ${\rm i^{th}}$ atom of the rigid body. The initial half-step advanced angular momentum can be expressed as

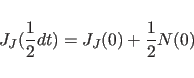$\begin{displaymath} J_J({1\over 2}dt)=J_J(0)+{1\over 2}N(0) \end{displaymath}$

(11.22)

and the first advancement of the center-of-mass coordinates can be written as

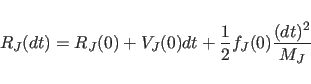$\begin{displaymath} R_J(dt)=R_J(0)+V_J(0)dt+{1\over 2}f_J(0){(dt)^2 \over M_J} \end{displaymath}$

(11.23)

Xplor-NIH 2025-03-21