Iteration

bit	Xplor-NIH	VMD-XPLOR

Xplor-NIH home Documentation

Next: Syntax of the Dynamics Up: Rigid-Body Coordinate Space Previous: Initialization

Iteration

After initialization, the center-of-mass variables are integrated using the three-step Verlet method: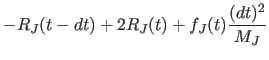

$\displaystyle R_J(t+dt)$	$\textstyle =$	$\displaystyle -R_J(t-dt)+2R_J(t)+f_J(t){(dt)^2 \over M_J}$	(11.24)
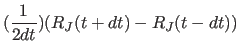$\displaystyle V_J(t)$	$\textstyle =$	$\displaystyle ({1\over 2dt})(R_J(t+dt)-R_J(t-dt))$	(11.25)

Friction terms are embedded in the force

The integration of rotational variables uses a different central difference expansion. The algorithm begins with the advancement of the Euler-Cayley parameters by ${1\over 2}dt$ , using the following four steps:

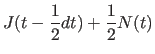$\displaystyle J(t)$	$\textstyle =$	$\displaystyle J(t-{1\over 2}dt)+{1\over 2}N(t)$	(11.26)
$\displaystyle J^B(t)$	$\textstyle =$	$\displaystyle {\bf A}(t)J(t)$	(11.27)
$\displaystyle \omega^B_{\alpha}$	$\textstyle =$	$\displaystyle J^B_{\alpha}(t)/I_\alpha \hspace*{1.0in}\alpha \in (x,y,z)$	(11.28)
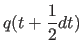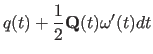$\displaystyle q(t+{1\over 2}dt)$	$\textstyle =$	$\displaystyle q(t)+{1\over 2}{\bf Q}(t)\omega'(t)dt$	(11.29)

Here

represents the angular momentum of a rigid body transformed to the body frame, and $\omega^B$ represents the transformed angular velocity; q is the four-vector (

). Finally, the torques are determined by

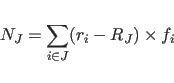$\begin{displaymath} N_J=\sum_{i\in J} (r_i-R_J)\times f_i \end{displaymath}$

(11.30)

Again, all frictional terms are embedded in the force

. These half-step calculations are necessary for the final, full-step update:

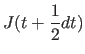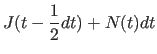$\displaystyle J(t+{1\over 2}dt)$	$\textstyle =$	$\displaystyle J(t-{1\over 2}dt)+N(t)dt$	(11.31)
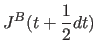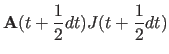$\displaystyle J^B(t+{1\over 2}dt)$	$\textstyle =$	$\displaystyle {\bf A}(t+{1\over 2}dt)J(t+{1\over 2}dt)$	(11.32)
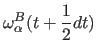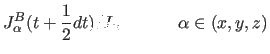$\displaystyle \omega^B_{\alpha}(t+{1\over 2}dt)$	$\textstyle =$	$\displaystyle J^B_{\alpha}(t+{1\over 2}dt)/I_\alpha \hspace{0.5in} \alpha \in (x,y,z)$	(11.33)
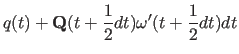$\displaystyle q(t+dt)$	$\textstyle =$	$\displaystyle q(t)+{\bf Q}(t+{1\over 2}dt)\omega'(t+{1\over 2}dt)dt$	(11.34)

The velocities of individual atoms, which are necessary for the friction evaluation, are determined using the angular velocities of the rigid bodies. The velocity due to rotation alone is determined in the body frame, then transformed into the lab frame and added to the translational velocity of the center of mass:

$\begin{displaymath} v_i(t)=V_J(t)+{\bf A_J}^{-1}\left[\begin{array}{c} z^B_{i}\o... ...\ y^B_{i}\omega^B_{x}-x^B_{i}\omega^B_{y} \end{array} \right] \end{displaymath}$

(11.35)

Finally, the atom positions are updated for the next energy evaluation using the new center-of-mass positions and the new Euler-Cayley parameters:

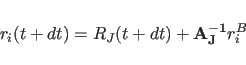$\begin{displaymath} r_i(t+dt)=R_J(t+dt)+{\bf A^{-1}_{J}}r^B_{i} \end{displaymath}$

(11.36)

The rigid-body dynamics routine can be run in one of three modes: FREE, LANGevin, or TCOUpling. The FREE mode simply allows frictionless dynamics, the LANGevin mode adds friction- and bath-dependent random forces, and TCOUpling uses the method of Berendsen et al. (1984). The coordinates (and velocities) are affected by using a nonzero friction coefficient in the Langevin dynamics algorithm with zero random forces. The friction coefficient is computed by the program from the equation

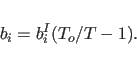$\begin{displaymath} b_i=b_i^I (T_o/T -1). \end{displaymath}$

(11.37)

where

is given by the FBETa atom property. Note that FBETa is by default zero; that is, FBETa has to be specified in order to use TCOUpling. The target temperature

is specified by the TBATh parameter.

If the simulation involves light rigid groups such as water molecules, it is recommended that a time step on the order of .25 fsec be used. For heavier groups, time steps as large as 20 or 30 fsec are adequate.

Xplor-NIH 2025-11-07