U.S. flag

An official website of the United States government
  next up previous contents index  Xplor-NIH home Documentation

Next: Initialization Up: Molecular Dynamics Previous: Example: Run Langevin Dynamics


Rigid-Body Coordinate Space

Rigid-body dynamics solves Newton's equations of motion for rigid collections of atoms (Goldstein, 1980). Atoms are collected into rigid groups, the motion of which is determined by summing the forces acting on all of a group's elements and integrating the rigid-body equations of motion. The atomic masses $m_i$ are defined through the topology statement (Section 3.1.1). The initial atomic coordinates are taken from the main coordinate set (atom properties X,Y,Z). After completion of a rigid-body dynamics run, the main coordinate set contains the coordinates of the last step. The initial velocities are taken from the atom properties VX,VY,VZ. They must be initialized outside the rigid-body dynamics statement. After completion of a rigid-body dynamics run, the velocities of the last step are stored in the atom properties VX, VY, VZ.

After completion of the molecular dynamics calculation, the partial energy terms for the last molecular dynamics step are stored in the appropriate symbols. The name of the symbols is given by $$<$energy-term$>$ (see Section 4.5). The overall energy (Eq. 4.1) is stored in the symbol $ENER; the rms gradient is stored in $GRAD. The value of the second energy function (Eq. 4.26) is returned in the symbol $PERT. In addition, the following symbols are declared: $TEMP, $TOTE, and $TOTK, which are respectively the temperature, total energy, and kinetic energy.

X-PLOR's implementation of rigid-body molecular dynamics follows the algorithm described by Head-Gordon and Brooks (1991). The algorithm treats each group as a continuous mass distribution located at the center-of-mass position defined by

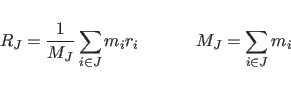\begin{displaymath} R_J={1\over M_J}\sum_{i\in J} m_ir_i\hspace{0.5in}M_J=\sum_{i\in J} m_i \end{displaymath} (11.11)

and characterized by its inertia tensor ${\bf I_J}$, which has as elements
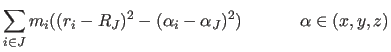$\displaystyle I_{\alpha\alpha}$ $\textstyle =$ $\displaystyle \sum_{i\in J} m_i((r_i-R_J)^2-(\alpha_i-\alpha_J)^2) \hspace{0.5in} \alpha \in (x,y,z)$ (11.12)
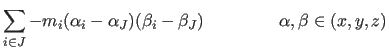$\displaystyle I_{\alpha\beta}$ $\textstyle =$ $\displaystyle \sum_{i\in J} -m_i(\alpha_i-\alpha_J)(\beta_i-\beta_J) \hspace{0.65in} \alpha,\beta \in (x,y,z)$ (11.13)

Here the index J labels the rigid bodies, and the summation index $i$ runs over all atoms comprising a particular group.


Subsections
next up previous contents index
Next: Initialization Up: Molecular Dynamics Previous: Example: Run Langevin Dynamics   Contents   Index
Xplor-NIH 2025-03-21