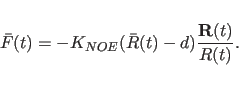| bit | Xplor-NIH | VMD-XPLOR |
|---|
|
| Xplor-NIH home Documentation |
Next: Antidistance Restraints Up: Distance Restraints Previous: Example for a High
Refinement Using Time-Averaged Distance Restraints
NMR-derived structures can be refined with time-averaged NOE distance
restraints (Torda, Scheek, and van Gunsteren, 1990; Pearlman and Kollman, 1991; Torda, Scheek, and van Gunsteren, 1989)
using
the TAVErage statement. In this method the NOE restraint potential is
changed so that distance restraints derived from NOE are applied to
the time-average of each distance, rather than each instantaneous
distance. Thus R in Eqs. 20.7,
20.10, 20.12, 20.13
is replaced by an averaged distance
In practice, a slightly different form of the above equation is used
to calculate ![]() ; for a discrete number of time points, the
equation becomes
; for a discrete number of time points, the
equation becomes
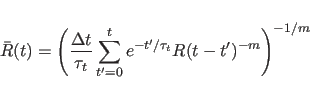 |
(20.23) |
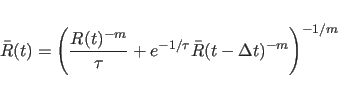 |
(20.24) |
The initial values for ![]() can be set to either the current
distances,
can be set to either the current
distances, ![]() ,
or to the restraint distances,
,
or to the restraint distances, ![]() , using the TAVErage RESEt statement
(CURRent or CONStraint).
, using the TAVErage RESEt statement
(CURRent or CONStraint).
The force associated with each NOE restraint is normally taken to be
the spatial derivative of the energy term, e.g. for a square well
potential,
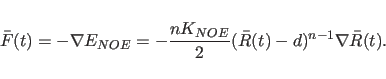 |
(20.25) |
![\begin{displaymath}
\nabla \bar{R}(t) = \frac{1}{\tau}
\left[\frac{\bar{R}(t)}{R(t)}\right]^{m+1} \nabla R(t).
\end{displaymath}](img722.png) |
(20.26) |
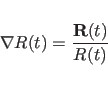 |
(20.27) |
Note the fourth-power term with respect to
Integrating this force term leads to a time-dependent NOE energy term, hence this force is nonconservative. In X-PLOR the force field can be chosen by setting FORCe to either CONServative (Eq. 20.28) or NONConservative (Eq. 20.29).
X-PLOR can also accumulate running-averages of the distances using the
RAVErage statement. The running-average is calculated from
![\begin{displaymath}
< R(t) > = \left(\frac{1}{t}\sum_0^t[R(t-t')]^{-3}\delta t'\right)^{-1/3}
\end{displaymath}](img731.png) |
(20.30) |
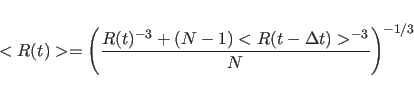 |
(20.31) |
See Section 38.10 for an example for time- and running-averages.
Xplor-NIH 2025-11-07

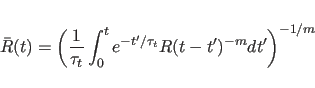
![\begin{displaymath}
\bar{F}(t) = - \frac{K_{NOE}}{\tau}(\bar{R}(t) - d)
\left[\frac{\bar{R}(t)}{R(t)}\right]^4 \frac{{\bf R}(t)}{R(t)}
\end{displaymath}](img728.png)