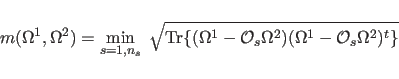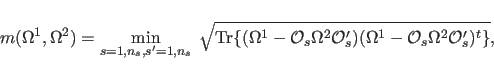| bit | Xplor-NIH | VMD-XPLOR |
|---|
|
| Xplor-NIH home Documentation |
Next: Syntax Up: Molecular Replacement Previous: Molecular Replacement
Rotation Search
X-PLOR performs conventional rotation searches in Patterson
space.
The real-space Patterson search method of Huber (1985) is employed.
The stationary Patterson map P2 is computed from the observed
intensities by fast Fourier transformation on the specified grid.
The Patterson map P1 to be rotated is computed from
either the observed intensities (self-rotation search) or
from a search model (cross-rotation search).
Note that the rotation search routine takes the layout of the map
P1 as it was written using the xrefin map statement
(see Section 16.1).
In most cases, the layout of P1 will look like
this:
EXTEnd=BOX XMIN=-45.0 XMAX=45.0 YMIN=-45.0 YMAX=45.0 ZMIN=0.0 ZMAX=30.0where one makes use of the centrosymmetry and 30.0 is the maximum vector length. Patterson vectors are selected according to the value of the Patterson map at the particular grid point (THREshold) and according to the distance from the grid point to the origin (RANGe). Of this selected subset of Patterson vectors, only the strongest NPEAKs Patterson vectors are chosen for the rotation search.
The selected Patterson vectors are rotated using
Eulerian angles (![]() ,
, ![]() ,
, ![]() ) as defined
by Rossmann and Blow (1962), pseudo-orthogonal Eulerian angles
as defined by Lattman (1985),
or spherical polar angles (
) as defined
by Rossmann and Blow (1962), pseudo-orthogonal Eulerian angles
as defined by Lattman (1985),
or spherical polar angles (
![]() )
(see Section 2.4 for the conventions).
The
Lattman angles are related to
the Eulerian angles by
)
(see Section 2.4 for the conventions).
The
Lattman angles are related to
the Eulerian angles by
| (19.1) | |||
The
The values of the Patterson map P2 at the positions of the rotated Patterson vectors of map P1 are computed by linear eight-point interpolation (Nordman, 1980).
For each
sampled orientation ![]() the product function
the product function
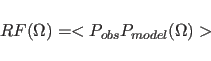 |
(19.2) |
Upon completion of the rotation function,
all sampled grid points are sorted with respect to their product
correlation value,
and a simple peak search is carried out using the matrix metric defined
in Brünger (1990). For two given rotation matrices
![]() , the metric is defined as
, the metric is defined as
i.e., the metric assumes the crystal symmetry for both Patterson maps P1 and P2. In the case of space group
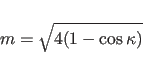 |
(19.5) |
Two RF grid points are considered
as being in the same cluster
if the corresponding
rotation matrices yield
![]() . For
example, if
. For
example, if ![]() is set to 0.25, matrices belong to the same
cluster if they can be transformed by a rotation of 10
is set to 0.25, matrices belong to the same
cluster if they can be transformed by a rotation of 10![]() or less around a certain axis.
The incorporation of crystallographic symmetry in Eq. 19.3
ensures that clusters of grid points at the boundaries of the asymmetric
unit of the RF are treated properly.
or less around a certain axis.
The incorporation of crystallographic symmetry in Eq. 19.3
ensures that clusters of grid points at the boundaries of the asymmetric
unit of the RF are treated properly.
This peak search removes grid points
that are close to grid points
with larger RF values. It is not a true peak search, but rather
reduces the number of points to be checked by subsequent analysis.
The reduced set of the highest
grid points is written to a specified file. For example, if ![]() is set to 0.25, the file will contain grid points that are
mutually different by at least 10
is set to 0.25, the file will contain grid points that are
mutually different by at least 10![]() .
This file will be read by the
.
This file will be read by the ![]() -refinement procedure described
below. The value for
-refinement procedure described
below. The value for
![]() should be chosen to be less than the
radius of convergence of the
should be chosen to be less than the
radius of convergence of the ![]() -refinement (around 10
-refinement (around 10![]() ).
It should be noted that the peak search procedure
maps the grid points into
an asymmetric unit of the rotation function.
).
It should be noted that the peak search procedure
maps the grid points into
an asymmetric unit of the rotation function.
Subsections Xplor-NIH 2025-11-07